How the Forces Work
Devlog #3 — 2025-02-20 Introduction >> Modeling the Real World >> The Algorithm >> Source Code
Introduction
As explained in the last devlog, the physics in Magnet Game behave differently than real-world physics. However, my goal is to make it the systems act as intuitively as possible. After around a year of playing with different ideas, I believe I have finally found the best algorithm to represent this. Note that all the below information is subject to change before the game's release. This algorithm works well for the current interactions, but new mechanics might warrant a full revamp of the algorithm.
Modeling the Real World
The most intuitive way to simulate the real world is to, well, model it after the real world. Very early on, I decided on using a force system to move magnets. I wanted to include:
- External forces, for magnetic force from non-connected magnets and objects getting pushed.
- Internal forces on a deformable body, for connected magnets moving each other.
- Normal forces, to prevent objects from moving through walls.
The Algorithm
By far the most challenging part of developing Magnet Game so far has been resolving the math. Having recently algorithmized this math, I want to share an abstracted version here.
First, all forces and writeable data are cleared. This lets us start each tick with a fresh environment. Next, magnets Mi are connected to surrounding magnets M0...3 of colors c into the following sets:
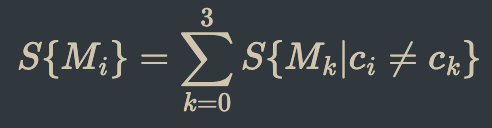
Magnet Connection Equation
This just means that all surrounding magnets with the opposite color (red/blue) as the base magnet are attached and placed in a member set of the base magnet. Each magnet also stores the recursive connection set, defined by the set of all sets in Mi.
The user's input is then applied to the character magnet as a force vector, adding it to an array of all applied forces. The vector is scaled by a variable that controls how much to weight the user's input.
All magnets on the map generate magnetic fields that extend to nearby cells. In this step, the sum of those forces are applied as a property of each cell. The reason this happens instead of applying the forces to magnets directly is to future-proof the system for eventually adding particles that travel along the magnetic fields. Next, the forces are applied to each magnet with the following conditions:
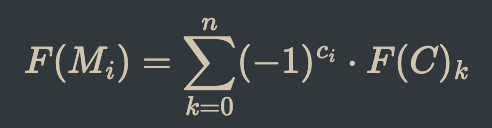
Cell Force to Magnet Equation
where C is the cell the magnet occupies and ci is 0 for blue magnets and 1 for red magnets.
The hardest part is next: distributing the forces to connected magnets. For this, I experimented with different values and equations for a long time, eventually settling on:
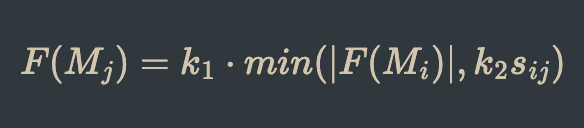
Force Distribution Equation
where Mi is the magnet distributing the force, Mj is the magnet accepting the force, constant k1 <= 1 and k2 depends on the direction of the force, and sij is the attraction strength between the magnets.
The next calculation is for pushing objects. If an object wants to occupy a cell, but that cell contains a moveable object that is not in the object's recursive connected magnet array, then the net force of the object is passed to the moveable object in the desired cell. This is done a few times to account for objects in rows and allows for non-magnetic objects (like a Rock) to be pushed.
At this point, a temporary net force is generated, which is what decides the magnet's "ideal location." This is what makes the little animation when a magnet tries to move, but can't, as seen below.

Ideal Movement Example
The player magnet on the top moves to the right and passes some of that force to the bottom magnet. The net force on the bottom magnet at this point is to the right, so it moves slightly in that direction. Then, when the Normal force is calculated below, the magnet realizes it can't move to it's ideal location and resets to its original location.
For the Normal force, the engine checks if a magnet's net force is occupying an immovable object. If it is, a force of the same magnitude in the opposite direction is applied to the magnet. This is done separately for both x and y directions to allow magnets to "slide" along walls. If the only wall that the net force occupies is on a corner, then the Normal force is calculated using:
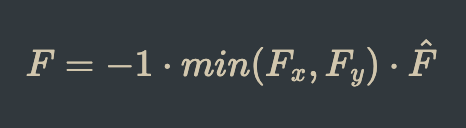
Normal Force Equation
which splits up the forces intuitively and pushes the magnet a bit more in the stronger direction.
The final calculation is generating a final net force, which is what the magnets will use to decide their movement (discussed in the next devlog). Instead of abstracting this process, I decided to share the source code, so feel free to check out this algorithm in the Source Code section below.
Source Code
Here is function for generating the final net force of map objects with some of the repetitive bits removed. It won't be plug and play, as it is based heavily on custom classes, but hopefully it provides a good framework for calculating the net force given a list of applied forces from various sources.
func final_net() -> void:
for gobj in map.moveable_gobjs:
var forces = gobj.applied_forces.filter(func(a): return a.type != Enumap.forcetype.EXT_NORMAL and a.type != Enumap.forcetype.INT_NORMAL)
var passer_dict : Dictionary = {}
for force in forces:
if force.passer not in passer_dict:
passer_dict[force.passer] = []
passer_dict[force.passer].append(force)
var max_x_forces_from_each_passer = []
for passer in passer_dict:
# Passer x
var passer_x_forces = passer_dict[passer].map(func(a): return a.vector.x)
var passer_pos_x_forces = passer_x_forces.filter(func(a): return a > 0)
var passer_neg_x_forces = passer_x_forces.filter(func(a): return a < 0)
var passer_pos_x_force = passer_pos_x_forces.max()
if passer_pos_x_force == null:
passer_pos_x_force = 0
var passer_neg_x_force = passer_neg_x_forces.min()
if passer_neg_x_force == null:
passer_neg_x_force = 0
max_x_forces_from_each_passer.append(passer_pos_x_force + passer_neg_x_force)
# Total x
var x_force = max_x_forces_from_each_passer.reduce(func(a, b): return a + b)
if x_force == null:
x_force = 0
elif x_force > 0:
x_force = min(x_force, max_x_forces_from_each_passer.max())
elif x_force < 0:
x_force = max(x_force, max_x_forces_from_each_passer.min())
# Repeat above sections for y_force, x_normal_force, and y_normal_force
# Game Logic
var final_x_force = 0
if x_force < 0:
if x_normal_force > 0:
final_x_force = min(x_force + x_normal_force, 0)
gobj.friction = max(abs(x_force - final_x_force) * friction_weighting, gobj.friction)
else:
final_x_force = x_force
# same for x_force > 0, repeat for y
gobj.net_force = Vector2(final_x_force, final_y_force)
